临床实验设计与分析
1. 临床试验概述
研究设计的就基本原则:随机、对照、重复(临床试验结果的可重复性)、均衡(控制其他混杂因素的偏倚或非处理因素的影响,如性别、年龄等)
统计设计:无偏性(减少非必要的偏倚)、最小变异性(各种因素对变异的贡献程度:把非观察效应去掉,留下处理效应)
2. 单因素方差分析
2.1 概念
方差分析(analysis of variance,ANNOVA)/F检验/变异数分析:比较不同组别的均数是否有统计学的差异,必须符合正态分布
注:单因素方差分析:要探讨的只有一个因素,不代表数据只有一处理个因素
2.2 计算
总变异 = 组间变异 + 组内变异(误差)
观察值效应 = 总平均效应 + 处理效应 + 随机误差效应
总变异:离均差平方和
组间变异:每一组平均值到总平均值的变异。包括处理因素的变异以及随机误差
组内变异:每个值到组内平均值的变异。
变异的分解:均方MS=离均差平方和/自由度
总自由度 = 组间自由度+组内自由度
F=MS组间/MS组内,F越大,表示组间差异贡献越大
2.3 应用条件
方差分析应用条件:
独立性:相互独立的随机样本,若不独立,某些因素可能在两个组别之间有一些共有的效应
正态性:符合正态分布
方差齐性:两个组别的离散程度变异程度是一样的,否则比较均值没有意义
检验方差齐性方法:
- bartlett检验
- levene检验 :用于对多总体方差进行齐性检验时,所分析的资料可以不具有正态性。
如果方差不齐,可以采用数据变换:
- 平方根反正弦变换
- 平方根变换(服从泊松分布)
- 对数变换(服从对数正态分布:抗体滴度、传染病潜伏期)
2.4 完全随机设计资料的方差分析
研究中只安排一个研究因素,同质的受试对象随机分配到各个处理组中。
- 随机分组
- 随机安排处理因素
满足独立性、正态性、方差齐性的,采用单因素方差分析one-way ANNOVA;
对两组情况也可以采用成对t检验;
对于非正态或/和方差不齐数据,可先进性变量变换,然后采用单向分类方差分析或采用Kruskal-Wills H检验。
2.5 多个样本均数间的多重比较
多重比较
H0:μ1=μ2=μ3
H1:μ1、μ2、μ3不全相等
如果方差分析结果拒绝H0,接受H1,则三个数不全相等,比较哪两个总体均数不等,要进行多个样本间两两比较,即多重比较。
两两t检验(做三组)在统计学上是不妥的,统计学结论都是概率性的,有犯错误的可能。
若进行6次t检验来检验4组数据平均值是否相同,每次犯I类错误的概率是α,则进行6次比较,犯I类错误概率为1-(1-α)^6,概率将上升。
多重比较方法
- LSD-t检验
- Dunnett-t检验
- SNK检验/q检验
3. 多因素方差分析
处理因素不止一个。
**析因分析:**不止包含两个因素单独的处理效应,还包括交互作用(一阶交互作用AB、BC、AC、二阶交互作用ABC)
- 单独效应:A因素固定时,B因素两个水平取值的差异;如图
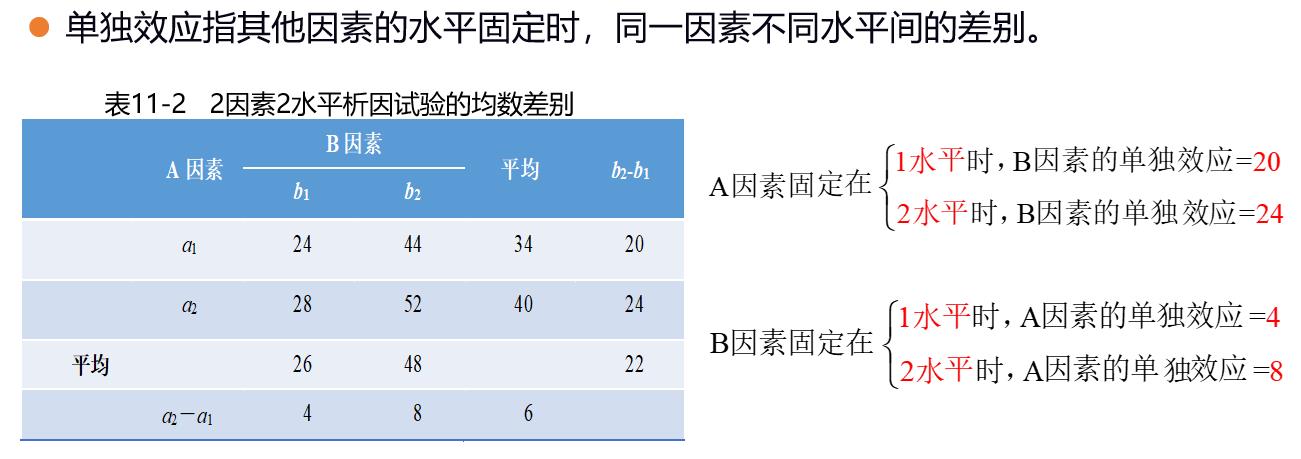 :
: - 主效应:不管A的水平,探讨B的效应,某一个因素各水平之间的差别;如图
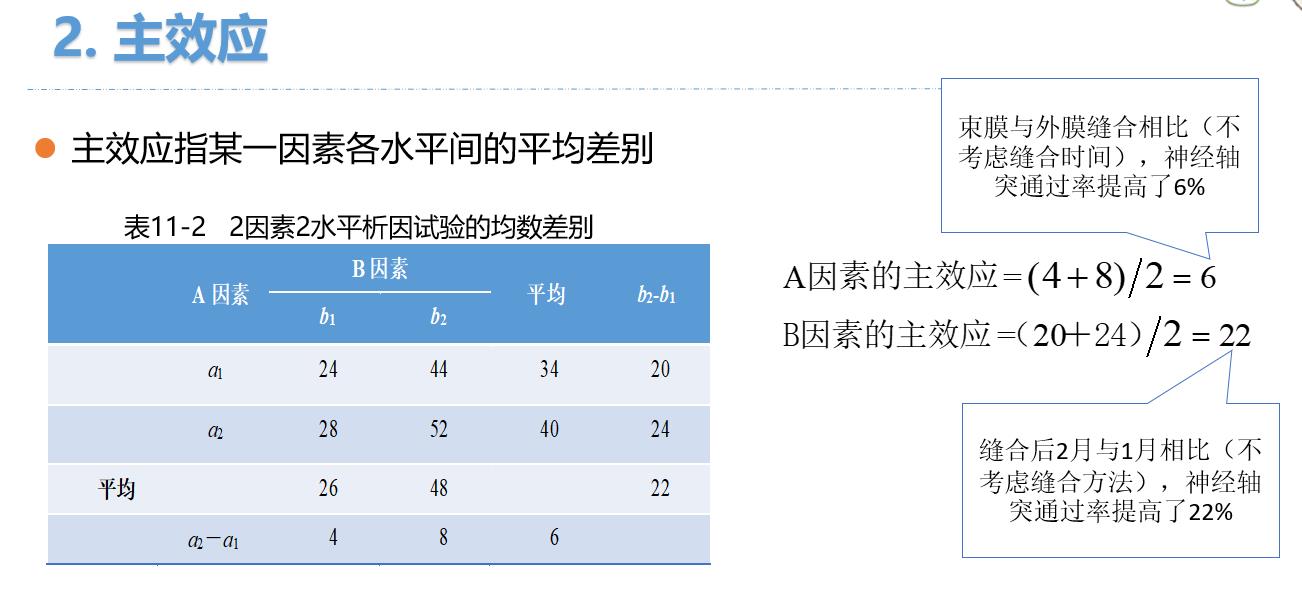
- 交互作用:不平行/交叉,可能有交互作用;如图

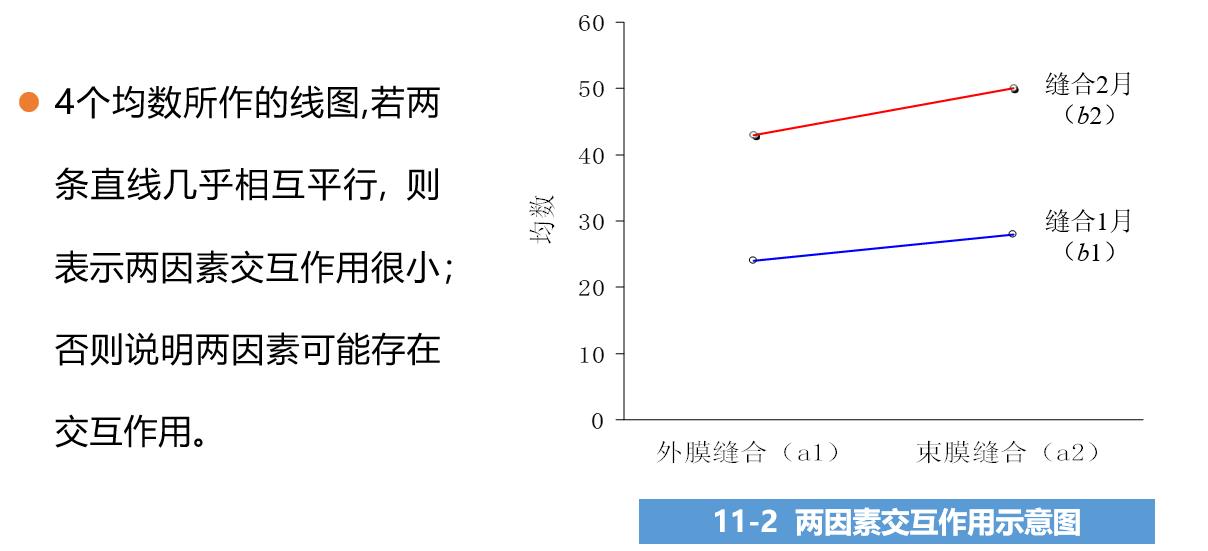
总变异SS总 = SS处理 + SS误差 = SSA + SSB + SSAB + SS误差
自由度V总 = V处理 + V误差 = VA + VB + VAB + V误差
嵌套设计
各因素按隶属关系系统分组,各因素水平没有交叉。A、B因素分别为一级、二级处理因素,例如一级实验因素为饲料的种类,二级实验因素为饲料的喂养量。计算方法如图:
还有正交设计、裂区设计等。
4. 协方差分析ANCOVA
4.1 协方差分析
协方差分析是将线性回归和方差分析结合起来。
协变量co-variant:
除处理因素外,与结局有关对观察指标有影响的变量,如性别、年龄、病情严重程度等。
例如观察降压药物对血压的影响时,患者的初始血压水平也对血压有影响,但患者血压的初始水平难以控制、但又会对结果造成影响,这样来说初始水平就是一个协变量。
协变量在组间分布不均衡,可能导致分析结果的偏倚。
使协变量组间均衡的方法:
随机分组;按协变量取值进行分层随机化(如40岁的人各个组都放几个);
在纳入标准中限定个体协变量取值,使所有受试者具有相同的协变量值。
注:即使组间均衡,若个体协变量差异较大,也会影响实验结果。
协变量分析、多重回归分析、分层分析
4.2 协方差分析的应用条件
- 方差分析的三个条件
- 独立性、正态分布、方差齐性
- 平行性:存在应变量对协变量的线性回归关系且斜率相同。
- 协变量的要求
- 连续变量
- 影响观察结局,但不能影响处理因素;
- 取值应在研究前被观察,或研究中观察,但不受处理的影响。
4.2 协方差分析模型
例如,研究体重正常或超重对胆固醇含量的影响:
自变量:正常/超重,二分类变量
协变量:年龄,难以控制的定量因素
应变量:胆固醇含量
应变量与协变量的关系:胆固醇含量与年龄的关系,如果与体重正常/超重有关,则不满足条件,不能做协方差分析。
协变量年龄与应变量的关系,在两组之间是一样的(斜率相同)。
分析模型
因此要研究体重正常者和超重者的血清胆固醇是否不同,即检验𝛽1是否为0。
协方差分析所需要进行的检验包含两步:
①对不同组别中应变量对协变量的回归系数是否相同进行检验,即平行性检验;
②若满足平行性假定,则进一步检验两组间应变量总体均数是否存在差异。
假设检验:
1.先检验应变量和协变量的关系 在自变量两个不同组之间是一样的(斜率一样)
2. 应变量和自变量的关系:两样本组总体均值差异检验
Fisher
karl pearson
student